Abstract
Our ability to use deep learning approaches to decipher neural activity would likely benefit from greater scale, in terms of both the model size and the datasets. However, the integration of many neural recordings into one unified model is challenging, as each recording contains the activity of different neurons from different individual animals.
In this paper, we introduce a training framework and architecture designed to model the population dynamics of neural activity across diverse, large-scale neural recordings. Our method first tokenizes individual spikes within the dataset to build an efficient representation of neural events that captures the fine temporal structure of neural activity. We then employ cross-attention and a PerceiverIO backbone to further construct a latent tokenization of neural population activities. Utilizing this architecture and training framework, we construct a large- scale multi-session model trained on large datasets from seven nonhuman primates, spanning over 158 different sessions of recording from over 27,373 neural units and over 100 hours of recordings.
In a number of different tasks, we demonstrate that our pretrained model can be rapidly adapted to new, unseen sessions with unspecified neuron correspondence, enabling few-shot performance with minimal labels. This work presents a powerful new approach for building deep learning tools to analyze neural data and stakes out a clear path to training at scale for neural decoding models.
Datasets & Challenges
We curated a multi-lab dataset with electrophysiological recordings containing spike trains from motor cortical regions. In total, we aggregated 178 sessions worth of data, with 29,453 units from the primary motor (M1), premotor (PMd), and primary somatosensory (S1) regions in the cortex of 9 nonhuman primates.
| Study | Regions | Tasks | # Individuals | # Sessions | # Units | # Spikes | # Behavior Timepoints |
|---|---|---|---|---|---|---|---|
| Perich et al. | M1, PMd | Center-Out, Random Target | 4 | 117 | 11,557 | 143M | 20M |
| Churchland et al. | M1 | Center-Out | 2 | 9 | 1,728 | 706M | 87M |
| Makin et al. | M1, S1 | Random Target | 2 | 47 | 14,899 | 123M | 15M |
| Flint et al. | M1 | Center-Out | 1 | 5 | 957 | 7.9M | 0.3M |
| NLB-Maze | M1 | Maze | 1 | 1 | 182 | 3.6M | 6.8M |
| NLB-RTT | M1, S1 | Random Target | 1 | 1 | 130 | 1.5M | 2.8M |
Table 1: Datasets used in this work
All of these neural recordings were collected while the animals performed various motor tasks that vary in their inherent complexity:

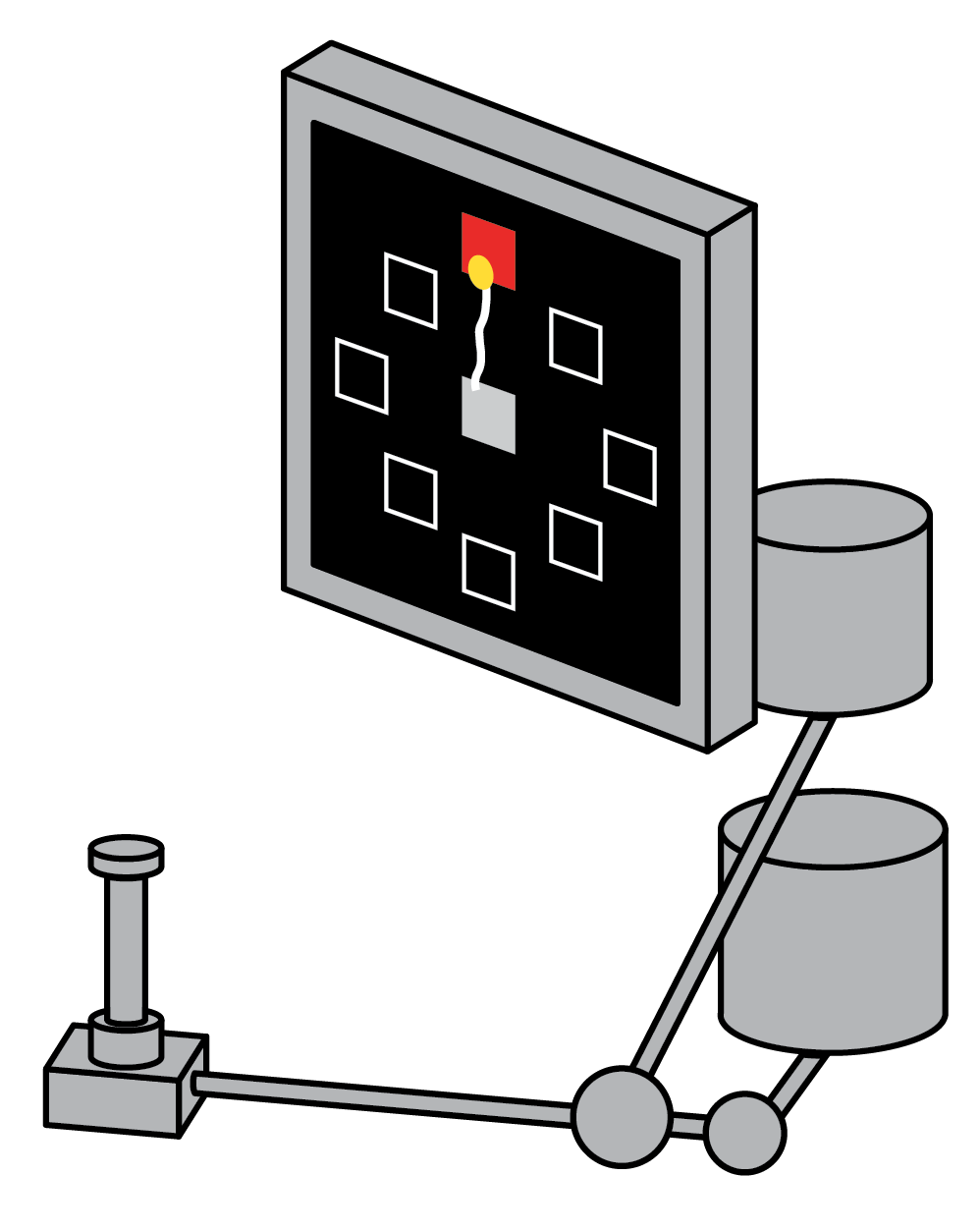

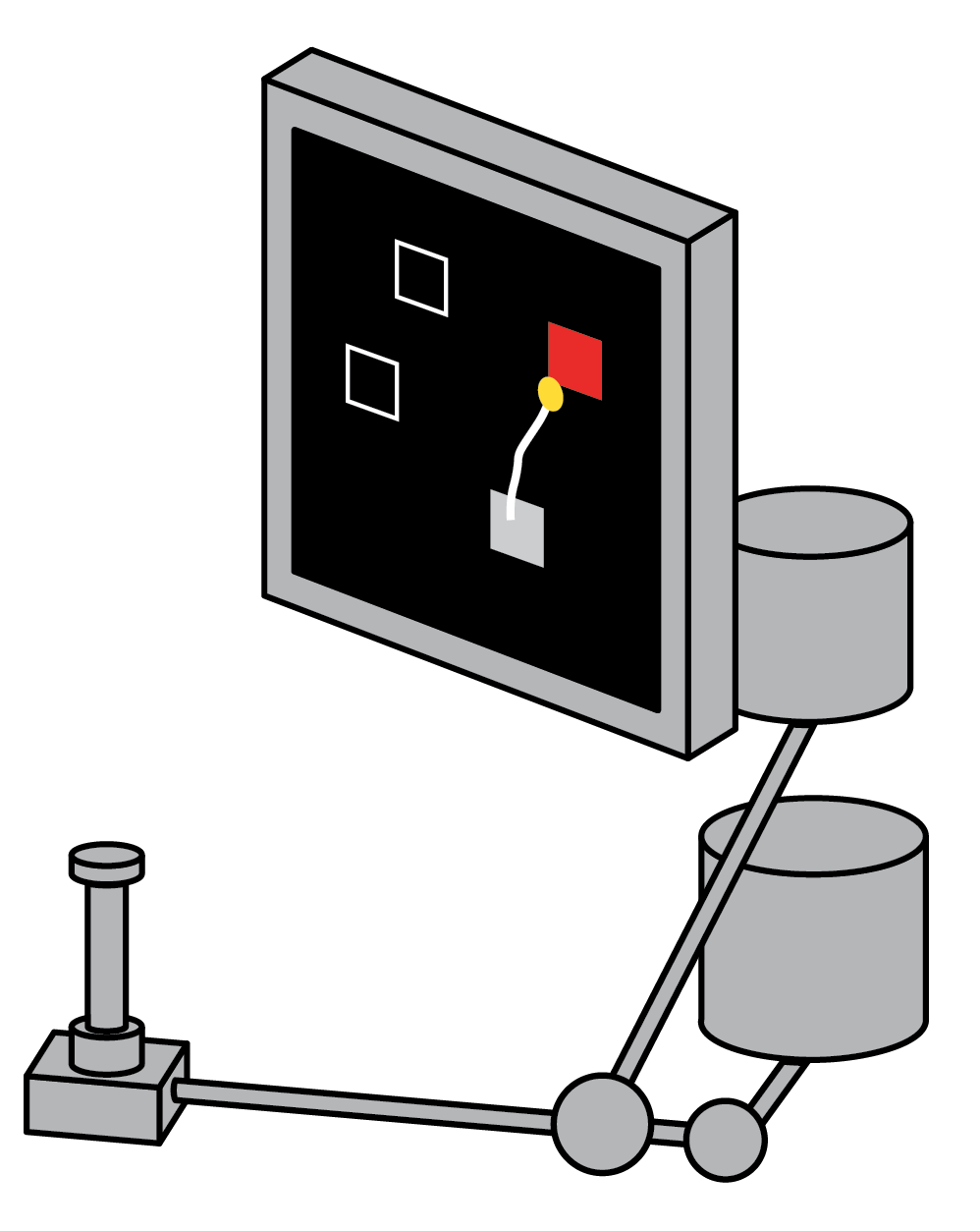

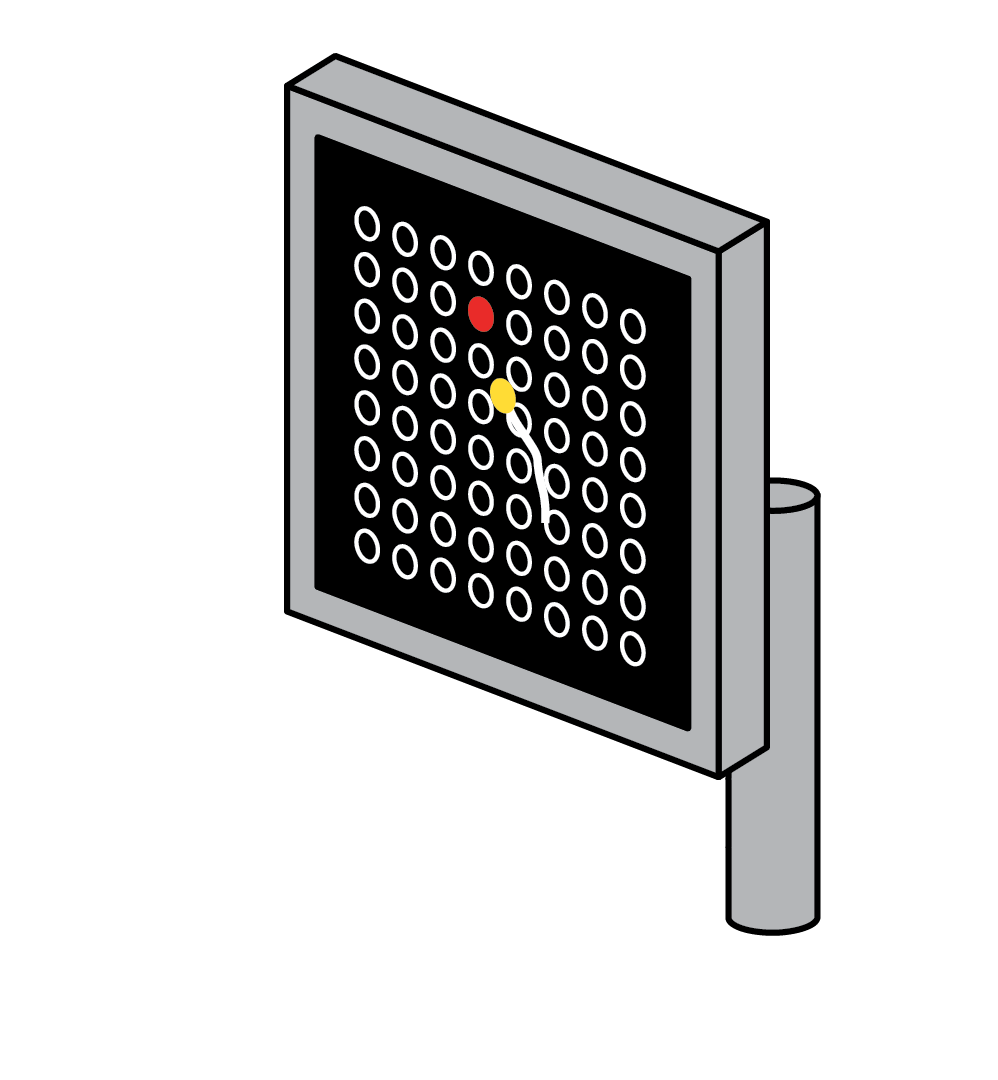

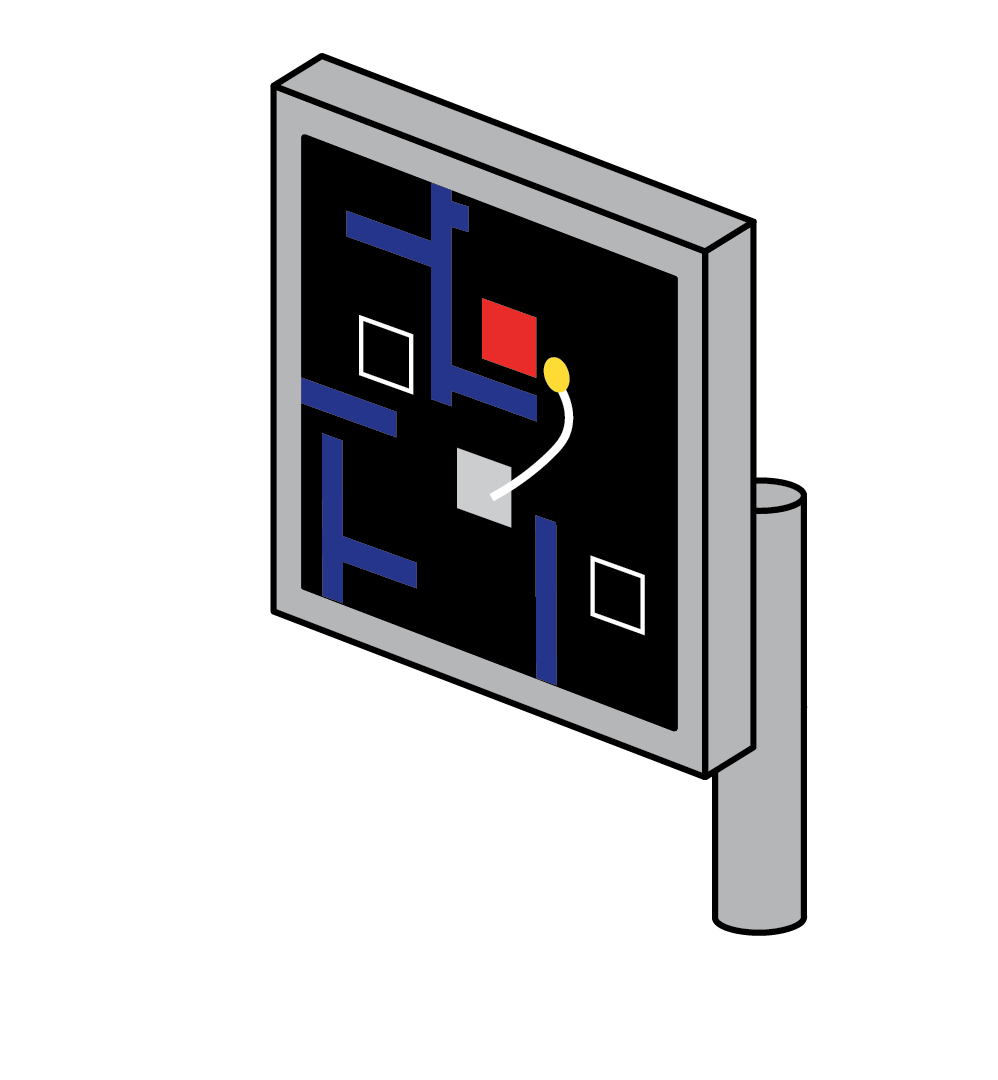
Maze task: In this task, a monkey performing reaches with instructed delays to visually presented targets while avoiding the boundaries of a virtual maze.
Challenges
Variability of neural recordings across days and individuals: Outside of knowing which region of the brain was implanted, the identity of the neurons that are recorded is unknown: we are dealing with unlabelled channels. This means that we don't know which neurons are being recorded from, or how many we are able to record.
Variablity in data processing: Different algorithms are used to process the electrophysiological recordings. Some datasets are spike-sorted, others are threshold-crossed. The quality and type of units will thus vary.
Heterogeneity of behavior across datasets: The datasets were collected from multiple labs, using different equipment, and with different experimental protocols. The studied motor tasks vary in their inherent complexity.
Variablity in sampling rate: The sampling rate at which these behaviors were recorded varies from lab to lab (100Hz to 1kHz).
Tokenization
Spike Tokenization
This aspect forms the core innovation of our research. In our approach to tokenizing neural population activity, each spike is represented as a token. In contrast to large language models (LLMs) that typically operate with a well-defined vocabulary, the concept of a corpus of "spike words" is less straightforward in neural activity. In our representation, each token encapsulates both the timing of a spike and the unique identity of the neuron from which it originates. As such, we represent our input as a set of tokens of arbitrary length.
 Try adding new spikes to one of the three units, by tapping on the Spikes plot below, and see how
new tokens are added.
Try adding new spikes to one of the three units, by tapping on the Spikes plot below, and see how
new tokens are added.
Behavior Query Tokens
The length of the hand velocity sequence will depend on the sampling frequency, which differs significantly across datasets. We propose a flexible mechanism for predicting outputs of varying lengths by querying our model one point at a time.
To account for variability in experimental conditions, we add a session-level embedding to every ouput query. The output query token is thus defined by its timestamp, and its corresponding learnable session embedding.
 Try querying the model at new timestamps, by tapping on the Query Timestamps plot below, and see
how the model responds.
Try querying the model at new timestamps, by tapping on the Query Timestamps plot below, and see
how the model responds.
Architecture
With our tokenization techniques, the problem of Neural Decoding boils down to learning a model that converts a sequence of spike tokens to a sequence of hand-velocities.
Our approach utilizes the Transformer architecture, recognized for its excellence in handling sequence-to-sequence transformations. Given the difference in number of tokens between input and output and the potentially large number of spikes, we've adopted the PerceiverIO architecture [Jaegle et al.] instead of the standard transformer [Vaswani et al.]. To inject token timestamps into the attention blocks, we use Rotary Position Embeddings [Su et. al.], which is a compute efficient way to ensure our model is invariant to absolute-time shifts.
1. Querying the Spike Train
We compress the variable-length sequence of spike-tokens into 256 latent tokens using a Cross-Attention transformer, which is queried by learned Latent Embeddings.
2. Attention in the Latent Space
The compressed latent tokens are processed by multiple Self-Attention transformer blocks. Since we're only working with 256 latents, this is very quick.
3. Querying the Latent Space
A sequence of output-query tokens, one for each behavior sample available in the trial, query the processed latents using a Cross-Attention transformer.
Latent Embeddings
Eight copies of 32 distinct learned embeddings. Each set of 32 is assigned a single timestamp, and these eight sets collectively span a duration of one-second, which is our selected maximum trial length.
Behavior Queries
Learned session embeddings allow our model to train on
data from multiple sessions, days, and labs, simultaneously.
The lack of any structural restrictions on query timestamps
allows us to train with datasets using different sampling
rates.
Training Results
In addition to showing that our proposed model outperforms other approaches on hand velocity decoding when trained on single-session datasets, we show that training a single model on all datasets jointly leads to improved performance across the board.
Sample fromAs shown in Figure 1, we find that the performance of the model increases with model size, and with the amount of data, and this despite the heterogeneity of the datasets.
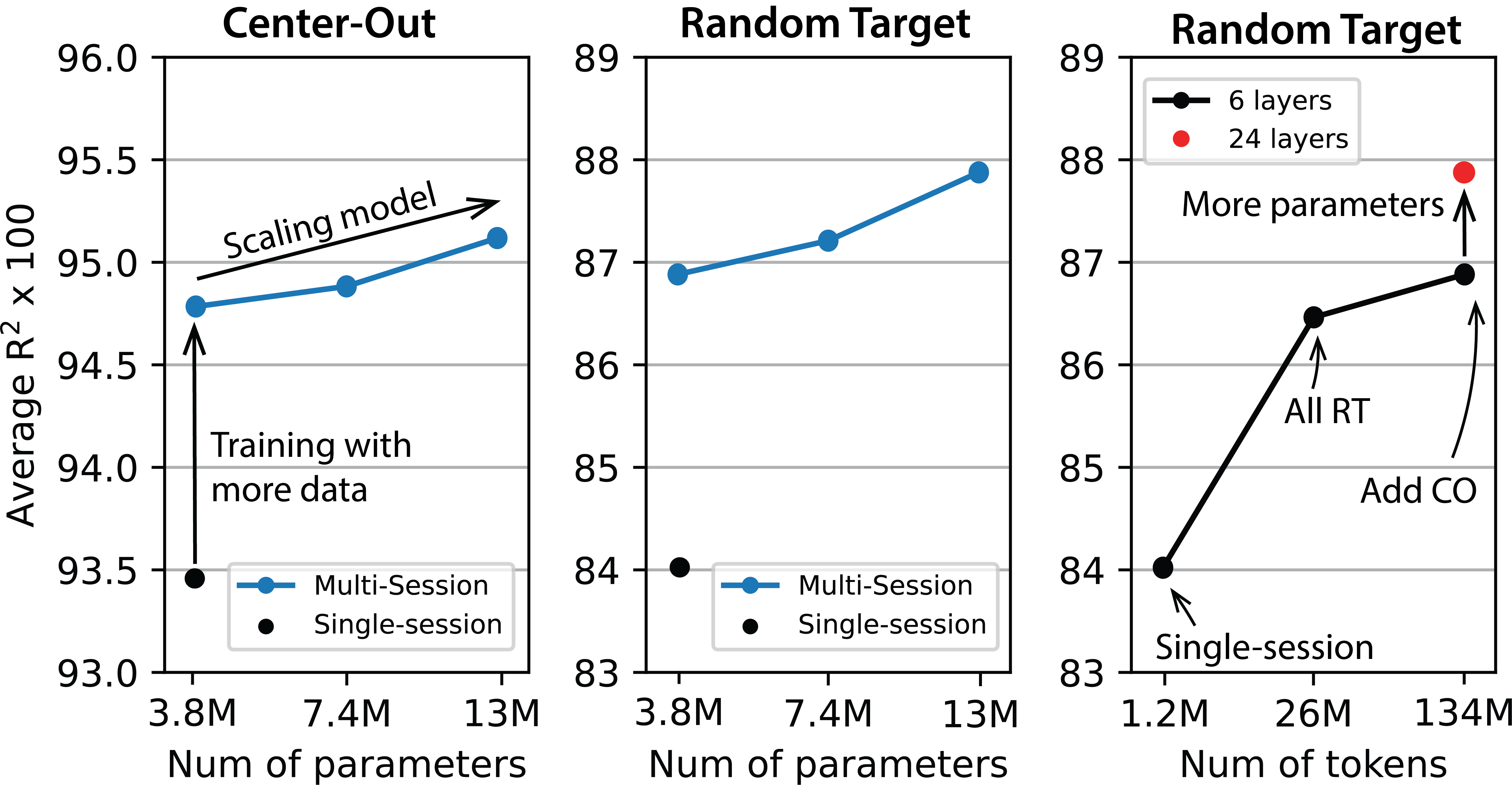
Figure 1: Scaling curves
Finetuning Results
Method
We can leverage our pretrained large model, POYO-1, for transfer on new datasets. We can use two different approaches:
1. Unit Identification: In order to transfer to a new neural population with previously unseen neurons, we need a way to first assign them a Unit Embedding. We leverage gradient descent to learn the embeddings of new units, while keeping the rest of the network weights fixed. Notably, the function that maps the neural population activity to behavior is unchanged and is simply transferred to the new dataset. In our experiments, we find that this approach is surprisingly effective and allows us to rapidly integrate new datasets into the same underlying model.
2. Full Finetuning: Start with POYO-1, and finetune all the weights.
Unit Identification in Action
Choose session:Results
| Method | Monkey C - CO (2) | Monkey T - CO (6) | Monkey T - RT (6) | NLB-Maze (1) | NLB-RTT (1) |
|---|---|---|---|---|---|
| Wiener Filter | 0.8860 ± 0.0149 | 0.6387 ± 0.0283 | 0.5922 ± 0.0901 | 0.7485 | 0.5438 |
| GRU | 0.9308 ± 0.0257 | 0.8041 ± 0.0232 | 0.6967 ± 0.1011 | 0.8887 | 0.5951 |
| MLP | 0.9498 ± 0.0119 | 0.8577 ± 0.0242 | 0.7467 ± 0.0771 | 0.8794 | 0.6953 |
| POYO-[Single-session] (from scratch) | 0.9682 ± 0.0111 | 0.9194 ± 0.0185 | 0.7800 ± 0.0702 | 0.9470 | 0.6850 |
| POYO-MP + Unit identification | 0.9675 ± 0.0079 | 0.9012 ± 0.0271 | 0.7759 ± 0.0471 | 0.8962 | 0.7107 |
| POYO-MP + Full finetune | 0.9708 ± 0.0116 | 0.9379 ± 0.0193 | 0.8105 ± 0.0561 | 0.9466 | 0.7318 |
| POYO-1 + Unit identification | 0.9677 ± 0.0096 | 0.9028 ± 0.0248 | 0.7788 ± 0.0548 | 0.9329 | 0.7294 |
| POYO-1 + Full finetune | 0.9683 ± 0.0118 | 0.9364 ± 0.0132 | 0.8145 ± 0.0496 | 0.9482 | 0.7378 |
Table 2: Behavioral decoding results for 16 sessions of neural recordings from four nonhuman primates. All the baselines and the single-session model are trained from scratch, while POYO-MP and POYO-1 are pretrained. The standard deviation is reported over the sessions.
Cite our work
If you find this useful for your research, please consider citing our work:@inproceedings{
azabou2023unified,
title={A Unified, Scalable Framework for Neural Population Decoding},
author={Mehdi Azabou and Vinam Arora and Venkataramana Ganesh and Ximeng Mao and Santosh Nachimuthu and Michael Mendelson and Blake Richards and Matthew Perich and Guillaume Lajoie and Eva L. Dyer},
booktitle={Thirty-seventh Conference on Neural Information Processing Systems},
year={2023},
} Georgia Institute of Technology,
2
Georgia Institute of Technology,
2  Mila,
3
Mila,
3  Université de Montréal,
Université de Montréal,
 McGill University,
5
McGill University,
5  CIFAR
CIFAR